LUMIÈRE - Dispersion et absorption

LUMIÈRE - Dispersion et absorption

Suivant sa fréquence, un rayonnement électromagnétique interagit différemment avec la matière. Un des aspects de ce phénomène est la dispersion, c’est-à-dire la variation de l’indice de réfraction de la substance en fonction de la longueur d’onde.

L’observation des faisceaux colorés émergeant d’un prisme éclairé en lumière blanche s’interprète en admettant cette loi de variation. Ce phénomène, appelé dispersion de réfraction, est une des causes de la mauvaise qualité des images données par les objectifs lorsqu’ils ne sont pas spécialement corrigés (aberrations chromatiques) et permet, en pratique, l’analyse de lumières complexes (spectroscopie).

De même, suivant sa fréquence, un rayonnement électromagnétique est plus ou moins absorbé par une substance dans laquelle il se propage. Nous verrons dans l’étude qui va suivre que dispersion et absorption sont des phénomènes liés et doivent être présentés ensemble. Il faut noter aussi qu’il existe un lien étroit entre émission et absorption, (cf. SPECTROSCOPIE, LUMIÈRE – Optique et LUMINESCENCE).

La variation de l’indice manifeste celle de la permittivité électrique du milieu qui, en électromagnétisme, lui est reliée de façon simple. Lorentz a complété cette théorie en faisant intervenir les constituants de la matière (atomes et molécules) qui entrent en vibration de façon différente suivant la fréquence du rayonnement. La permittivité, s’exprimant en fonction des caractéristiques de ces oscillateurs, dépend ainsi de la longueur d’onde. Réciproquement, l’étude expérimentale de la dispersion permet d’obtenir des renseignements sur la constitution de la matière.

La théorie moderne de la dispersion et de l’absorption fait appel à la mécanique quantique. Cependant, on utilisera la théorie électromagnétique qui est d’un emploi plus facile et permet une représentation satisfaisante de la plupart des phénomènes.

1. Dispersions normale et anormale: absorption

Un rayon lumineux traversant un prisme subit une déviation d’autant plus grande que l’indice de réfraction n , est plus élevé; on peut par suite mettre facilement en évidence la dispersion de réfraction par la méthode suivante, dite des spectres croisés.

Un objectif O (fig. 1) forme, d’une source blanche S, sensiblement ponctuelle, une image sur un écran E. Entre l’objectif et l’écran sont interposés un prisme A de petit angle à arête horizontale et d’indice n , qui produit une déviation verticale sensiblement proportionnelle à (n 漣 1), et un réseau R à traits verticaux, introduisant une déviation horizontale sensiblement proportionnelle à. On observe sur l’écran une trace colorée représentant la fonction (n 漣 1) = f ().

En général, la déviation croît du rouge au violet, l’indice est donc une fonction décroissante de la longueur d’onde; on dit alors que la dispersion est normale. Au contraire, si la substance constituant le prisme est absorbante dans un certain domaine de longueurs d’onde, on trouve que l’indice est une fonction croissante de; la dispersion est alors anormale.

La dispersion anormale peut être observée au voisinage des raies d’absorption de certains gaz, en utilisant la méthode des spectres croisés, le montage expérimental étant celui de la figure 2 a.

On éclaire à l’aide d’un arc au charbon A et d’un condenseur C, une fente horizontale ¹ placée au foyer objet d’un objectif L¹. Un objectif L² en forme une image sur la fente d’entrée verticale ² d’un spectroscope qui donne un spectre de très faible hauteur. Entre L¹ et L², on place un bec Bunsen B dont la flamme, dirigée par une petite gouttière G, a la forme d’un prisme d’arête horizontale. Une fente D limite la hauteur du faisceau entre L¹ et L². Si l’on place, par exemple, du sodium métallique dans G, il se vaporise et forme dans la flamme un prisme de vapeur. Lorsque la densité de celle-ci est suffisante, il apparaît dans le spectre une bande sombre correspondant aux raies D absorbées par cette vapeur; les variations d’indice se traduisent par un déplacement de cette bande, qui présente l’allure de la courbe de dispersion (fig. 2 b).

Les courbes de dispersion sont souvent bien représentées par des expressions de la forme:

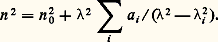Il y a autant de termes, en plus de n ⁰², que de régions d’absorption, chacune d’elles étant caractérisée par un coefficient a ⁱ . Cette relation n’est pas applicable au voisinage immédiat deⁱ , car elle donne pour n ² des valeurs infinies. Nous verrons que la théorie permet de tourner cette difficulté.

La relation se simplifie si les régions d’absorption sont assez éloignées du domaine exploré. Ainsi, si est grand devant les longueurs d’ondeⁱ , on peut écrire:

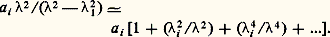En arrêtant le développement au troisième terme, on obtient pour n la formule de Cauchy:

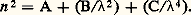Si est petit devantⁱ , on écrit:

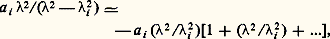et l’addition de ces termes à ceux de la relation précédente donne une formule due à Briot:

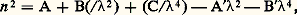qui, appliquée par exemple au domaine visible, permet de tenir compte de l’influence sur la dispersion des bandes d’absorption infrarouges et ultraviolettes.

2. Indice et polarisabilité

Rappelons que, dans un milieu matériel où règne un champ électrique つ, apparaît, si elle n’existe pas déjà, une polarisation, c’est-à-dire que chaque élément de volume d 精 du milieu est, ou devient, un petit doublet électrique de moment は 練d 精, par suite du déplacement, sous l’influence du champ, des charges électriques qu’il contient.

Si l’on passe de ce point de vue microscopique au point de vue macroscopique de Maxwell, on définit le vecteur induction électrique っ:

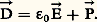Entre la polarisation は d’un milieu diélectrique et le champ つ qui règne à l’intérieur, on doit avoir une relation vectorielle du type:

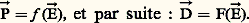L’hypothèse la plus simple, valable dans beaucoup de milieux isotropes, consiste à poser:

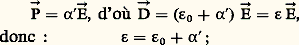見 est appelé susceptibilité.

Il existe une relation simple entre 﨎 et n :

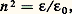d’où:

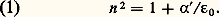Considérons un milieu comportant N molécules identiques par unité de volume. Chacune d’elles, sous l’action du champ つ, devient un dipôle de moment ら = 見 つ, 見 étant la polarisabilité de ce type de molécule. Le moment par unité de volume est alors: face="EU Arrow" は = 見 つ, et la relation (1) devient:

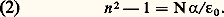Cette relation montre que la variation de n avec la longueur d’onde doit être attribuée à une variation de la polarisabilité.

Pour essayer d’en préciser le mécanisme, partons du modèle moléculaire consistant en un ensemble d’oscillateurs harmoniques. On suppose que les lois de la mécanique newtonienne sont applicables aux atomes et à leurs constituants.

Soit un corpuscule électrisé de masse m et de charge q , qui se déplace sous l’action d’un champ électrique つ. Par suite de son mouvement, il sera soumis à une force de frottement proportionnelle à sa vitesse, et à une force de rappel tendant à le ramener à sa position d’équilibre, proportionnelle à son élongation ひ. L’équation de son mouvement est de la forme:

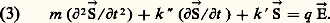Si la force q つ n’existait pas, la charge q , écartée de sa position d’équilibre, y reviendrait en effectuant des oscillations amorties. En l’absence d’amortissement, la pulsation aurait pour valeur:

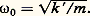Cette charge q , déplacée de ひ, est équivalente à un dipôle électrique de moment:

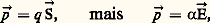d’où:

Pour obtenir 見, il faut connaître ひ, donc résoudre l’équation (3), ce qui implique le calcul préalable du champ électrique つ qui règne à l’intérieur de la matière. Ce calcul est très souvent compliqué, il se simplifie dans certains cas que nous allons étudier.

3. Étude théorique de la dispersion normale

Ce type de dispersion se produisant dans les zones de transparence, il est possible de négliger dans l’expression (3) la force d’amortissement k (d ひ/dt ) dont la participation n’est importante qu’au voisinage des bandes d’absorption, ce qui correspond aux fréquences de résonance des oscillateurs.

Gaz ou vapeurs

Dans les substances telles que les gaz ou les vapeurs, le champ つ agissant sur les électrons peut être confondu avec le champ de l’onde primaire, ce qui revient à négliger les champs créés par la polarisation des molécules. Dans ces conditions, l’équation (3), devient, si つ = つ^m sin 諸t :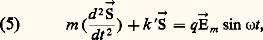

et admet une solution de la forme:

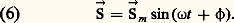En portant cette solution dans l’équation (5), on obtient:

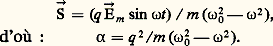La relation (2) devient:

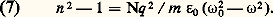Sur la courbe n ² = f ( 諸), de la figure (3), on constate que la dernière relation perd toute signification physique lorsqu’on s’approche de 諸⁰. Ce résultat n’a d’ailleurs rien de surprenant, car on suppose être loin d’une bande d’absorption; or 諸⁰ s’identifie avec la pulsation des ondes électromagnétiques absorbées par la substance. L’indice n’a pas de valeur réelle pour 諸⁰ 麗 諸 麗 諸¹, 諸¹ étant obtenu par n ² = 0, soit:

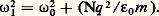La partie de la courbe en pointillé correspond aux ondes électromagnétiques qui ne peuvent pas se propager dans le milieu, car elles sont totalement absorbées (cf. chap. 5).

On généralise cette étude dans le cas de plusieurs types d’oscillateurs. Ainsi, on suppose qu’une même molécule contient a ¹, résonateurs de charges q ¹ de masse m ¹ et de pulsation propre 諸¹, a ² de constantes q ², m ², etc. La relation (6) devient:

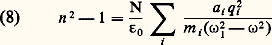Cette relation peut se transformer en exprimant 諸 en fonction de la longueur d’onde. On obtient alors la formule de Sellmeier:

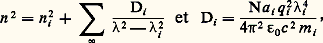c étant la célérité de la lumière et n size=1^秊 étant la valeur de l’indice lorsque la longueur d’onde tend vers l’infini.

Liquides et solides

Dans les substances telles que les liquides ou les solides, où le nombre N de molécules par unité de volume devient des milliers de fois plus grand que dans les gaz, on ne peut plus appliquer les relations précédentes obtenues en négligeant le champ électrique crée par la polarisation des molécules. Cette simplification n’étant plus possible, il est nécessaire, pour trouver le champ agissant, de faire la somme du champ de l’onde primaire et de ceux créés par les molécules polarisées. Un calcul plus exact, qui suppose toutefois qu’il n’y ait pas d’interactions entre les molécules, donne la relation de Lorentz-Lorenz:

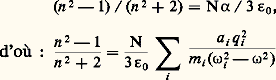relation qui n’est pas valable au voisinage d’une bande d’absorption.

En remarquant que le second membre est proportionnel à la densité d du milieu, cette expression peut s’écrire:

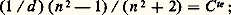c’est la loi de variation de l’indice avec la densité.

Cette loi n’est d’ailleurs pas très bien vérifiée expérimentalement, ce qui montre qu’il faut tenir compte, dans le calcul du champ local, de la contribution de toutes les molécules. Cependant, dans le cas des gaz, l’indice restant voisin de 1, cette formule se réduit à la relation de Gladstone:

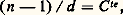qui permet de calculer avec une bonne approximation les variations de l’indice d’un gaz avec la température et la pression.

4. Origines de la polarisation suivant le domaine spectral

La polarisation des diélectriques peut avoir des origines diverses. Considérons, par exemple, une molécule diatomique, donc constituée de deux atomes différents A¹ et A². Par suite de leur interaction, il y a redistribution des électrons, donc déplacement des charges dans la liaison entre A¹ et A², et les centres de gravité des charges positives et négatives ne sont plus confondus: cette molécule possède un moment dipolaire dirigé suivant l’axe de symétrie A¹ et A². Ce moment étant permanent, la molécule est dite polaire.

Sous l’influence d’un champ électrique, la polarisation changera suivant deux mécanismes différents:

– par orientation de la molécule qui, assimilable à un dipôle, tourne pour s’aligner avec le champ; cette polarisation est dite dipolaire , et n’existe que pour les molécules polaires ;

– par déplacement des charges; si ce sont les atomes qui modifient leur distance, il y a variation du moment dipolaire de la molécule – si celui-ci existe – ou création d’un moment dipolaire induit – si la molécule n’est pas du type polaire (A¹ et A² identiques) –, la polarisation est dite atomique ; si ce sont les nuages d’électrons qui sont déplacés par rapport aux noyaux positifs des atomes, la polarisation est électronique .

Suivant la fréquence du champ appliqué, un certain type de polarisation devient prépondérant.

1. Dans l’infrarouge lointain et le domaine hertzien, l’origine de la polarisation est du type dipolaire. Dans le cas des gaz, les forces de frottement étant faibles, les molécules peuvent tourner librement. Si la pulsation de l’onde est voisine de la fréquence propre de rotation 諸⁰ des molécules, il se produit un phénomène de résonance et la variation de l’indice est semblable à celle de la figure 3, 諸⁰ étant situé dans la gamme des basses fréquences.

Dans le cas des liquides, il faut tenir compte d’une force de frottement d’origine visqueuse, qui entraîne l’existence d’un temps de relaxation t ⁰. Si le champ appliqué a une période T très supérieure à t ⁰, les molécules ont le temps de s’orienter. Si la fréquence augmente, la rotation des dipôles est de plus en plus déphasée par rapport au champ, pour finalement cesser lorsque T est très inférieur à t ⁰. Par suite, l’indice décroît lorsque 諸 augmente.

2. Dans le domaine des rayons X, les fréquences, de l’ordre de 10¹⁹ à 10²⁰ Hertz, sont beaucoup plus grandes que les fréquences propres les plus élevées, ce qui permet de négliger 諸ⁱ dans la relation (8) qui devient:

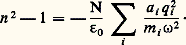Dans cette somme, la contribution des atomes sera négligeable devant celle des électrons dont la masse est beaucoup plus faible que celle des noyaux atomiques: la polarisation est du type électronique.

Si l’atome contient Z électrons de masse m et de charge e , cette relation devient:

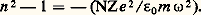On obtient par exemple pour le cuivre n ² = 1 漣 2 練 10⁵, n est toujours très voisin de l’unité, ce qui interdit en pratique l’utilisation de lentilles et de prismes dans l’optique des rayons X.

3. Dans le domaine spectral s’étendant de l’ultraviolet au proche infrarouge, la polarisation est d’origine à la fois électronique et atomique. Ainsi, toutes les molécules polyatomiques possèdent des bandes d’absorption dans l’ultraviolet et dans l’infrarouge, les premières étant dues aux électrons et les autres aux atomes. La courbe de la figure 4 montre l’évolution de l’indice de réfraction de NaCl solide en fonction de la longueur d’onde et fait apparaître deux bandes d’absorption: l’une vers 0,2 猪m, d’origine électronique, et l’autre vers 35 猪m, d’origine atomique.

5. Dispersion anormale des diélectriques: absorption

Cette dispersion apparaît au voisinage des bandes d’absorption des diélectriques. Dans ces régions, on ne peut pas négliger le terme d’amortissement k de l’équation (3). On cherche une solution de la forme complexe:

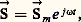le champ agissant étant:

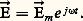L’équation devient:

En portant cette valeur de 見 dans la relation (2) et en généralisant comme pour la relation (8), on obtient la relation: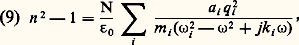

qui reste valable lorsqu’il y a différents résonateurs.

L’indice est donc une grandeur complexe dont la signification physique apparaît aisément en considérant la propagation d’une onde dans ce milieu, suivant une direction Oz . On a:

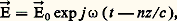l’indice n étant complexe, donc de la forme:

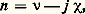l’expression précédente devient:

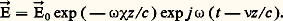On voit qu’au cours de sa propagation, cette onde s’atténue. Cette absorption est liée à la valeur de 﨑 que l’on appelle indice d’extinction, l’indice de réfraction étant 益.

En remplaçant n ² par ( 益 漣 j 﨑)² et en séparant partie réelle et partie imaginaire dans la relation (9), on obtient les formules de Ketteler-Helmholtz:

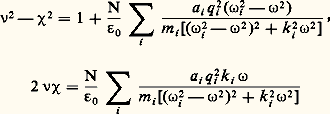Pour interpréter ces formules, on considère un milieu ne comportant qu’une seule région d’absorption et de faible densité, par exemple un gaz sous faible pression, afin que l’indice de réfraction 益 soit voisin de l’unité. Les relations précédentes deviennent alors:

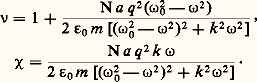Si la zone d’absorption est étroite, 諸⁰ est voisin de 諸, et on peut écrire:

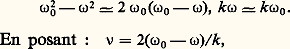on obtient:

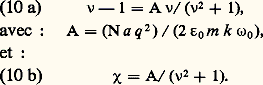Les courbes a et b de la figure 5 représentent la variation de 益 漣 1 et de 﨑 en fonction de 益. La courbe 﨑 = f ( 益) représente une raie d’absorption dont le maximum est situé en 諸 = 諸⁰ et a pour valeur A. Ainsi, par mesure de l’absorption de la substance, peut-on déduire A.

6. Dispersion et absorption dans les métaux

En étudiant la propagation d’une onde électromagnétique sinusoïdale dans un conducteur, on introduit une constante diélectrique complexe 﨎 qui s’exprime en fonction de la conductibilité 塚 par la relation:

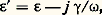﨎 ayant pour origine la polarisation due aux charges liées (courant de déplacement), la partie imaginaire provenant des électrons libres (courant de conduction).

En portant dans l’équation (1), on obtient:

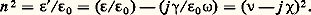En identifiant, on tire:

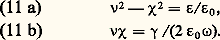L’étude expérimentale de l’indice n en fonction de la longueur d’onde conduit à un désaccord important entre les résultats obtenus et les prévisions théoriques. Ainsi, pour le mercure, les mesures donnent 益﨑 = 4,5 et les relations (11) 益﨑 = 19 (pour = 0,59 猪). Pour expliquer cet écart, on doit, comme pour les diélectriques, faire appel à la théorie électronique.

La théorie électronique appliquée aux diélectriques a permis de généraliser la relation (9) donnant la dispersion de l’indice, dans le cas où les électrons sont soumis à la fois à une force de rappel et à une force de frottement. Si on applique la même relation aux métaux, on fait apparaître deux termes: l’un, relatif aux électrons de conduction, considérés comme libres, s’obtient en faisant k ⁱ = 0, donc 諸ⁱ = 0 dans l’équation (9); l’autre, relatif aux électrons liés. On obtient, ainsi l’expression (12):

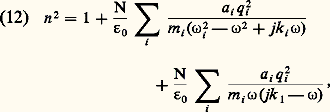qui peut se simplifier suivant le domaine spectral et la substance étudiée.

Pour discuter cette relation, on considère une substance ne possédant qu’un type d’électrons libres et pas de charges liées. Si e est la charge de l’électron, la relation (12) devient:

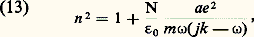ce qui permet d’exprimer 益 et 﨑:

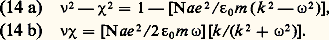– Dans le domaine infrarouge, où 諸 est petit devant k , on peut simplifier les relations (14) et, en comparant (14 b) à (11 b), on tire:

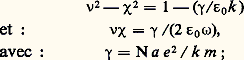et, comme k 礪礪 諸, on peut écrire:

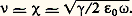Cette relation a été vérifiée expérimentalement sur des métaux du type alcalin qui remplissent assez bien les conditions de ce calcul. Cette vérification a été faite en mesurant le facteur de réflexion qui est lié par une relation simple à 益 et 﨑.

– Dans le domaine ultraviolet, on néglige k devant 諸 et la relation (13) devient:

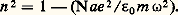L’indice est réel, et on peut prévoir une fréquence critique 諸^c pour laquelle n devient nul. Si 諸 礪 諸^c , le métal est transparent, mais n 麗 1.

– Dans le domaine visible, les simplifications précédentes ne sont plus valables et il est nécessaire de revenir à la relation complète (12) qui tient compte des diverses sortes d’électrons libres, ce qui n’a été envisagé que par S. Roberts en 1955. Il a repris la théorie de Drude qui, incomplète, donnait des résultats très différents de l’expérience. Ainsi, pour les métaux de transition, par exemple ceux du groupe du fer, il faut faire intervenir deux espèces d’électrons de conduction, et trois pour le nickel.

Encyclopédie Universelle. 2012.